Concreto Armado
Definições, um pouco de história, e conceitos fundamentais para o desenvolvimento do tema (fck, módulo de elasticidade, coeficiente de poison, efeito Rüsh, diagrama tensão deformação e fluência) - Publicado em Abril/2020
Diagrama tensão-deformação parábola-retângulo
NBR 6118: "Para tensões de compressão menores que 0,5 fc, pode-se admitir uma relação linear entre tensões
e deformações, adotando-se para módulo de elasticidade o valor secante dado pela expressão constante em 8.2.8"
(expressão e curvas apresentadas na aba Eci/Ecs).
"Para análises no estado-limite último, podem ser empregados o diagrama tensão-deformação
idealizado mostrado na Figura 8.2..."
(diagrama apresentado a seguir).
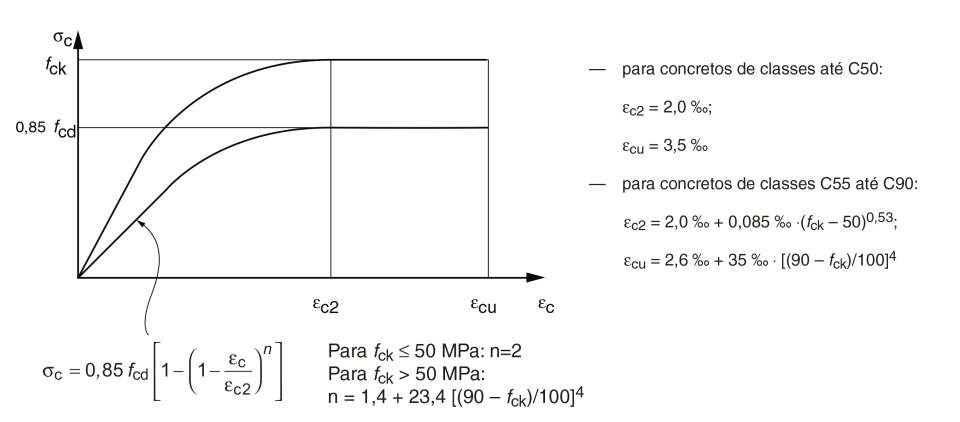
Referência: NBR 6118 - Item 8.2.10.1, Página 26
Observações:
- εcu é a deformação específica de encurtamento do concreto na ruptura;
- εc2 é a deformação específica de encurtamento do concreto no início do patamar plástico;
- A máxima tensão de projeto "fcd" é minorada em 15% (0,85.fcd) devido ao Efeito Rüsh;
Nos gráficos a seguir podemos comparar as curvas para diversificados fck.
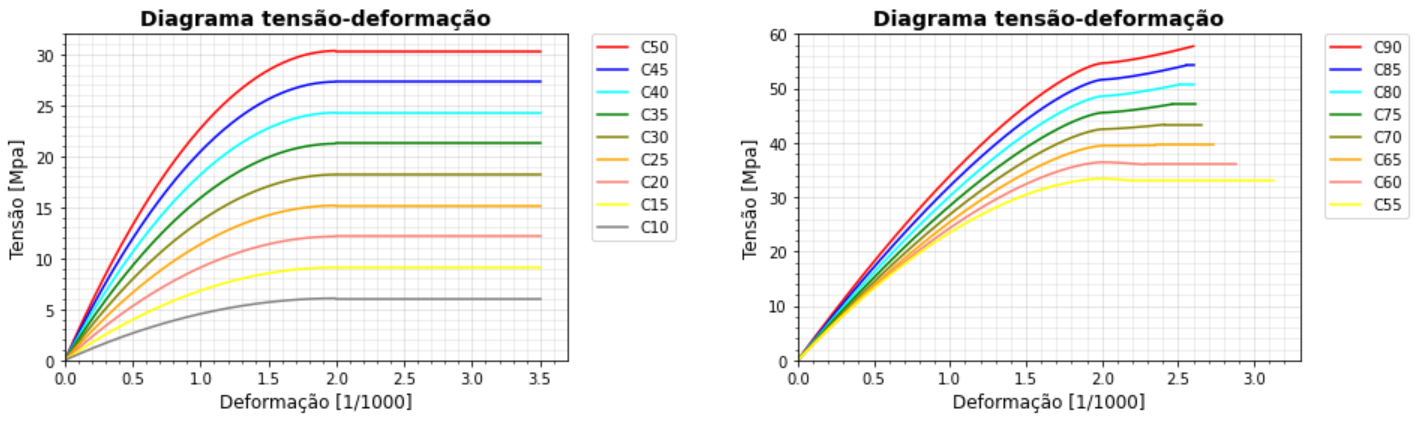
Diagrama tensão-deformação retangular
Conforme especificado em norma podemos utilizar um diagrama retangular simplificado como forma de facilitar o dimensionamento, e ilustrado a seguir para uma seção transversal qualquer.
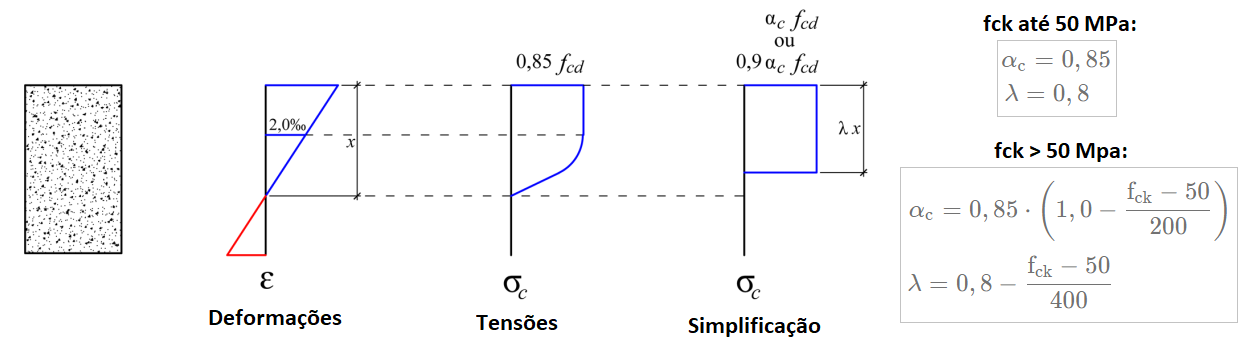
Considerações:
- x refere-se a linha neutra;
- λ é calculado em função da resistência característica do concreto (fck);
- As tensões são calculadas em função de αc , que também é função da resistência do concreto;
- Na curva da esquerda, observamos as deformações variando de acordo com a altura do bloco (compressão para direita e tração para a esquerda), observando que x é um ponto de tensões nulas (inversão de compressão para tração);
- Na curva central, temos o diagrama tensão-deformação parábola-retângulo para as tensões sobre o bloco (real);
- Na curva da direita, temos uma simplificação do diagrama tensão-tensão deformação para efeito de dimensionamento;
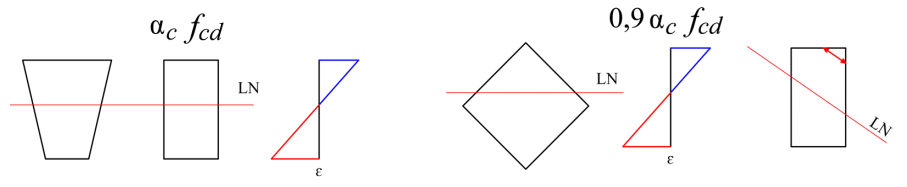
Importante observar que o uso de αc ou 0,9 . αc depende do formato da seção e posicionamento da linha neutra, sendo que para seções onde ocorre um alargamento na direção do centro aplicamos o fator de minoração de 10% (αc é devido ao efeito rüsh). A figura a seguir ilustra a utilização deste fator.
Scripts Python para geração dos diagramas tensão-deformação
#Diagrama Tensão Deformação Concreto até 50MPa
import matplotlib.pyplot as plt
import numpy as np
cor=['red','blue','cyan','green','olive','orange','salmon','yellow','gray']
concreto=['C50','C45','C40','C35','C30','C25','C20','C15','C10']
fcks=[50,45,40,35,30,25,20,15,10]
tensao=[]
deformacao=[]
indice=0
for fck in fcks:
cont_def = 0
while (cont_def <= 2):
deformacao.append(cont_def)
tensao.append(0.85*(fck/1.4)*(1-(1-(cont_def/2))**2))
cont_def = cont_def + 0.01
plt.plot(deformacao,tensao,color=cor[indice], label=concreto[indice])
x=[2,3.5]
y=[tensao[len(tensao)-1],tensao[len(tensao)-1]]
plt.plot(x,y,color=cor[indice])
deformacao=[]
tensao=[]
indice=indice+1
plt.legend(bbox_to_anchor=(1.05, 1),loc=2, borderaxespad=0.,)
# Show the major grid lines with dark grey lines
plt.grid(b=True, which='major', color='#666666', linestyle='-', alpha=0.2)
# Show the minor grid lines with very faint and almost transparent grey lines
plt.minorticks_on()
plt.grid(b=True, which='minor', color='#999999', linestyle='-', alpha=0.2)
plt.xlim(0, 3.7)
plt.ylim(0, 32)
plt.xlabel("Deformação [1/1000]", size = 12)
plt.ylabel("Tensão [Mpa]", size = 12)
plt.title("Diagrama tensão-deformação",
fontdict={'family': 'sans-serif',
'color' : 'black',
'weight': 'bold',
'size': 14})
plt.show
#Diagrama Tensão Deformação Concreto de 55MPa até 90MPa
import matplotlib.pyplot as plt
import numpy as np
cor=['red','blue','cyan','green','olive','orange','salmon','yellow']
concreto=['C90','C85','C80','C75','C70','C65','C60','C55']
fcks=[90,85,80,75,70,65,60,55]
tensao=[]
deformacao=[]
indice=0
for fck in fcks:
cont_def = 0
n=1.4+23.4*((90-fck)/(100))**4
ec2=1000*((2/1000)+((0.085/1000)*(fck-50)**0.53))
ecu=1000*((2.6/1000)+((35/1000)*(((90-fck)/100)**4)))
while (cont_def <= ec2):
deformacao.append(cont_def)
tensao.append(0.85*(fck/1.4)*(1-(1-(cont_def/2))**n))
cont_def = cont_def + 0.01
plt.plot(deformacao,tensao,color=cor[indice], label=concreto[indice])
x=[ec2,ecu]
y=[tensao[len(tensao)-1],tensao[len(tensao)-1]]
plt.plot(x,y,color=cor[indice])
deformacao=[]
tensao=[]
indice=indice+1
plt.legend(bbox_to_anchor=(1.05, 1),loc=2, borderaxespad=0.,)
# Show the major grid lines with dark grey lines
plt.grid(b=True, which='major', color='#666666', linestyle='-', alpha=0.2)
# Show the minor grid lines with very faint and almost transparent grey lines
plt.minorticks_on()
plt.grid(b=True, which='minor', color='#999999', linestyle='-', alpha=0.2)
plt.xlim(0, 3.3)
plt.ylim(0, 60)
plt.xlabel("Deformação [1/1000]", size = 12)
plt.ylabel("Tensão [Mpa]", size = 12)
plt.title("Diagrama tensão-deformação",
fontdict={'family': 'sans-serif',
'color' : 'black',
'weight': 'bold',
'size': 14})
plt.show