Vetores

Vetores - Conceitos e Aplicação com Python

Publicado em março/2020

Para executar as operações matemáticas e plotar os vetores apresentadas a seguir foram utilizadas as bibliotecas NumPy (Numerical Python) e Matplotlib (geração de gráficos).

Grandezas Escalares

Definidas por um únicos valor númerico, usualmente associado a uma unidade de medida, como massa, comprrimento ou tempo.

Vetores

Além da magnitude (módulo, tamanho ou norma), necessitam de direção e sentido para serem definidos. Com três dimensões podemos definir um ponto no espaço, por exemplo, mas vetores podem ter N dimensões, sendo de forma geral um conjunto de escalares.

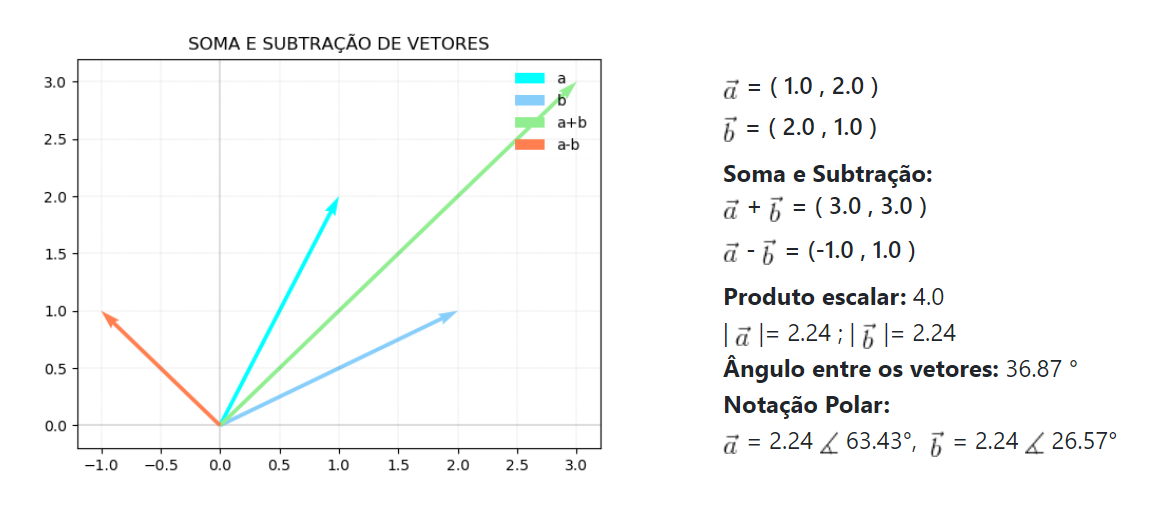
Soma e Subtração de Vetores

$\vec{a}$ =(x1,x2, ... , xn)
$\vec{b}$ =(y1,y2, ... , yn)
$\vec{a}$ + $\vec{b}$ =(x1+y1,x2+y2, ... , xn+yn)
$\vec{a}$ - $\vec{b}$ =(x1-y1,x2-y2, ... , xn+yn)

Produto Escalar

$\vec{a}$ =(x1,x2, ... , xn)
$\vec{b}$ =(y1,y2, ... , yn)
$\vec{a} \cdot \vec{b}$ =(x1⋅y1+x2⋅y2+ ... +xn⋅yn)

Produto Vetorial

$\vec{a} \times \vec{b} = \hat{u} .|a|.|b|.sen(\theta )$

θ → ângulo entre os vetores a e b (0° ≤ θ ≤ 180°) ;
$\hat{u}$ → vetor unitário perpendicular tanto a a quanto a b ;
|a| → módulo do vetor $\vec{a}$ ;
|b| → módulo do vetor $\vec{b}$ ;

Observar que existem dois vetores unitários que são perpendiculares à $\vec{a}$ e $\vec{b}$ simultaneamente, e o resultado depende da orientação do espaço vetorial. Pode utilizar a regra da mão direita para verificar o sentido correto (apontar o indicador na direção do primeiro operando e girar no sentido do menor ângulo até o segundo operando, sendo o vetor resultante na direção do polegar).

A figura a seguir disponível em https://pt.wikipedia.org/wiki/Produto_vetorial ilustra de forma bem clara o conceito de produto vetorial.

Interessante observar que o comprimento do vetor resultante do produto vetorial entre dois vetores é a área do paralelogramo definido por estes vetores ( no caso de produto misto resulta no volume do paralelepípedo formado pelos três vetores).

Para calcular o produto vetorial de forma computacional basta obter o determinante da matriz composta pelos 2 vetores juntamente com os respectivos vetores unitários em cada direção:

$\mathbf{a}\times\mathbf{b}=\det \begin{bmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ \end{bmatrix}$

Norma ou Módulo

É um número real que representa o comprimento do vetor.

$\vec{v} = (x_{1} , x_{2} , \cdots, x_{n})$

$|\vec{v}| = \sqrt{ x_{1}^{2} + x_{2}^{2} + \cdots + x_{n}^{2}}$

Ângulo Entre Vetores

$\cos (\theta ) = \frac{\vec{a} . \vec{b}}{|\vec{a}| . |\vec{b}|}$

Vetor Unitário

O versor é um vetor unitário que contém a informação relativa espacial das propriedades de direção e sentido, porém seu módulo é "1" e ele pode ser calculado da seguinte forma:

${\vec {u}}={\frac {\vec {v}}{|{\vec {v}}|}}$

Código Python

A seguir a função Python criada para efetuar os cálculo e retornar os valores para o template Django:

views.py

def algebraLinearVetores(request):
    if request.method == 'POST':
        matplotlib.use('Agg')
        x1 = float(request.POST.get('a'))
        y1 = float(request.POST.get('b'))
        x2 = float(request.POST.get('c'))
        y2 = float(request.POST.get('d'))
        cols = (['#00FFFF'], ['#87CEFA'], ['#90EE90'], ['#FF7F50'])
        nomes = ('a', 'b', 'a+b', 'a-b')
        # VETORES A E B
        vetor_a = np.array([x1,y1])
        vetor_b = np.array([x2,y2])
        # SOMA E SUBTRAÇÃO
        soma = vetor_a + vetor_b
        sub = vetor_a - vetor_b
        # PRODUTO ESCALAR
        produto_escalar = vetor_a.dot(vetor_b)
        # MÓDULO
        modulo_a = np.linalg.norm(vetor_a)
        modulo_b = np.linalg.norm(vetor_b)
        # VETOR UNITÁRIO
        ua = vetor_a/np.linalg.norm(vetor_a)
        ub = vetor_b / np.linalg.norm(vetor_b)
        # ANGULO ENTRE OS VETORES
        angulo=(180/np.pi)*(np.arccos(produto_escalar/(modulo_a*modulo_b)))
        # ANGULO PARA O EIXO X PARA A NOTAÇÃO POLAR
        angulo_a = (180 / np.pi) * (np.arccos(vetor_a.dot([1,0]) / (modulo_a * np.linalg.norm([1,0]))))
        if -1*vetor_a[1]>0: angulo_a = 360-angulo_a
        angulo_b = (180 / np.pi) * (np.arccos(vetor_b.dot([1, 0]) / (modulo_b * np.linalg.norm([1, 0]))))
        if -1 * vetor_b[1] > 0: angulo_b = 360 - angulo_b
        vetores = (vetor_a, vetor_b, soma, sub)
        # MAXIMO E MINIMO DOS EIXOS
        max_x = max(np.concatenate([vetor_a[0], vetor_b[0], soma[0], sub[0]], axis=None))
        max_y = max(np.concatenate([vetor_a[1], vetor_b[1], soma[1], sub[1]], axis=None))
        min_x = min(np.concatenate([vetor_a[0], vetor_b[0], soma[0], sub[0]], axis=None))
        min_y = min(np.concatenate([vetor_a[1], vetor_b[1], soma[1], sub[1]], axis=None))
        if max_x > 0 and min_x > 0: min_x = 0
        if max_x < 0 and min_x < 0: max_x = 0
        if max_y > 0 and min_y > 0: min_y = 0
        if max_y < 0 and min_y < 0: max_y = 0
        plt.title("SOMA E SUBTRAÇÃO DE VETORES")
        plt.xlim(min_x - 0.2, max_x + 0.2)
        plt.ylim(min_y - 0.2, max_y + 0.2)
        plt.grid(b=True, which='major', axis='both', color='808080', ls=':', lw=0.2)
        plt.axvline(x=0, color='#808080', zorder=0, lw=0.3)
        plt.axhline(y=0, color='#808080', zorder=0, lw=0.3)
        for i in range(len(vetores)):
            x = np.concatenate([[0, 0], vetores[i]])
            plt.quiver([x[0]], [x[1]], [x[2]], [x[3]], angles='xy', scale_units='xy', scale=1, color=cols[i],
                       label=nomes[i], alpha=None)
            plt.legend(loc=0, framealpha=0.01)
        imagem_buffer = io.BytesIO()
        plt.savefig(imagem_buffer, format="png")
        plt.cla()  # Clear axis
        plt.clf()  # Clear figure
        plt.close()  # Close a figure window
        image = base64.b64encode(imagem_buffer.getvalue()).decode('ascii')
        return render(request, 'algebraLinearVetores.html', {'image': image,
                                                             'a': str(round(vetor_a[0],2)),
                                                             'b': str(round(vetor_a[1],2)),
                                                             'c': str(round(vetor_b[0],2)),
                                                             'd': str(round(vetor_b[1],2)),
                                                             'e': str(round(soma[0],2)),
                                                             'f': str(round(soma[1],2)),
                                                             'g': str(round(sub[0],2)),
                                                             'h': str(round(sub[1],2)),
                                                             'i': str(round(produto_escalar, 2)),
                                                             'j': str(round(modulo_a, 2)),
                                                             'k': str(round(modulo_b, 2)),
                                                             'l': str(round(angulo, 2)),
                                                             'm': str(round(angulo_a, 2)),
                                                             'n': str(round(angulo_b, 2)),
                                                             'o': str(round(ua[0], 2)),
                                                             'p': str(round(ua[1], 2)),
                                                             'q': str(round(ub[0], 2)),
                                                             'r': str(round(ub[1], 2)),
                                                             })
    else:
        return render(request, 'algebraLinearVetores.html')

Carga da imagem no HTML

<img style="max-width : 450px" src="data:image/png;base64,{{ image }}"/>

Vetores - Conceitos e Aplicação com Python

$\vec{a}$ :

$\vec{b}$ :

Grandezas Escalares

Vetores

Soma e Subtração de Vetores

Produto Escalar

Produto Vetorial

Norma ou Módulo

Ângulo Entre Vetores

Vetor Unitário

Código Python

views.py

Carga da imagem no HTML